Unidad 3. Estructura de datos avanzados
3. Estructuras de datos avanzadas
3.1 Árboles
3.1.1. Definición del tipo de dato abstracto árbol binario
3.1.2. Definición de las operaciones sobre árboles binarios
3.1.3. Implantación de un árbol binario
3.2 Grafos
3.2.1 Definición del tipo de dato abstracto grafo
3.2.2 Operaciones sobre un grafo
3.2.3 Implantación de un grafo
Introducción
Existen estructuras de datos avanzadas, que se consideran así porque pueden tener una mayor cantidad de operaciones que las estructuras simples y manejan una organización en memoria más compleja. En su manejo pueden implicar también crear variantes de los tipos de datos simples.


Árboles
Cuando piensas en un árbol, como objeto de la vida real, imaginamos un tronco con una serie de ramas y hojas, también se puede visualizar que tanto las ramas como las hojas parten del tronco del árbol como una extensión o producto del mismo, en una relación dependiente o jerárquica. Existen tipos de datos que manejan esta relación jerárquica o dependencia entre los elementos para expresar significados particulares de acuerdo al contexto donde se aplican.
Definición de árboles

Aplicaciones de los árboles

Fuente: propia (2020)
Representación Genérica

Fuente: propia (2020)
Para comprender la estructura y funciones
de los árboles, es importante identificar los elementos que los conforman, los
cuales puedes revisar en la siguiente figura:
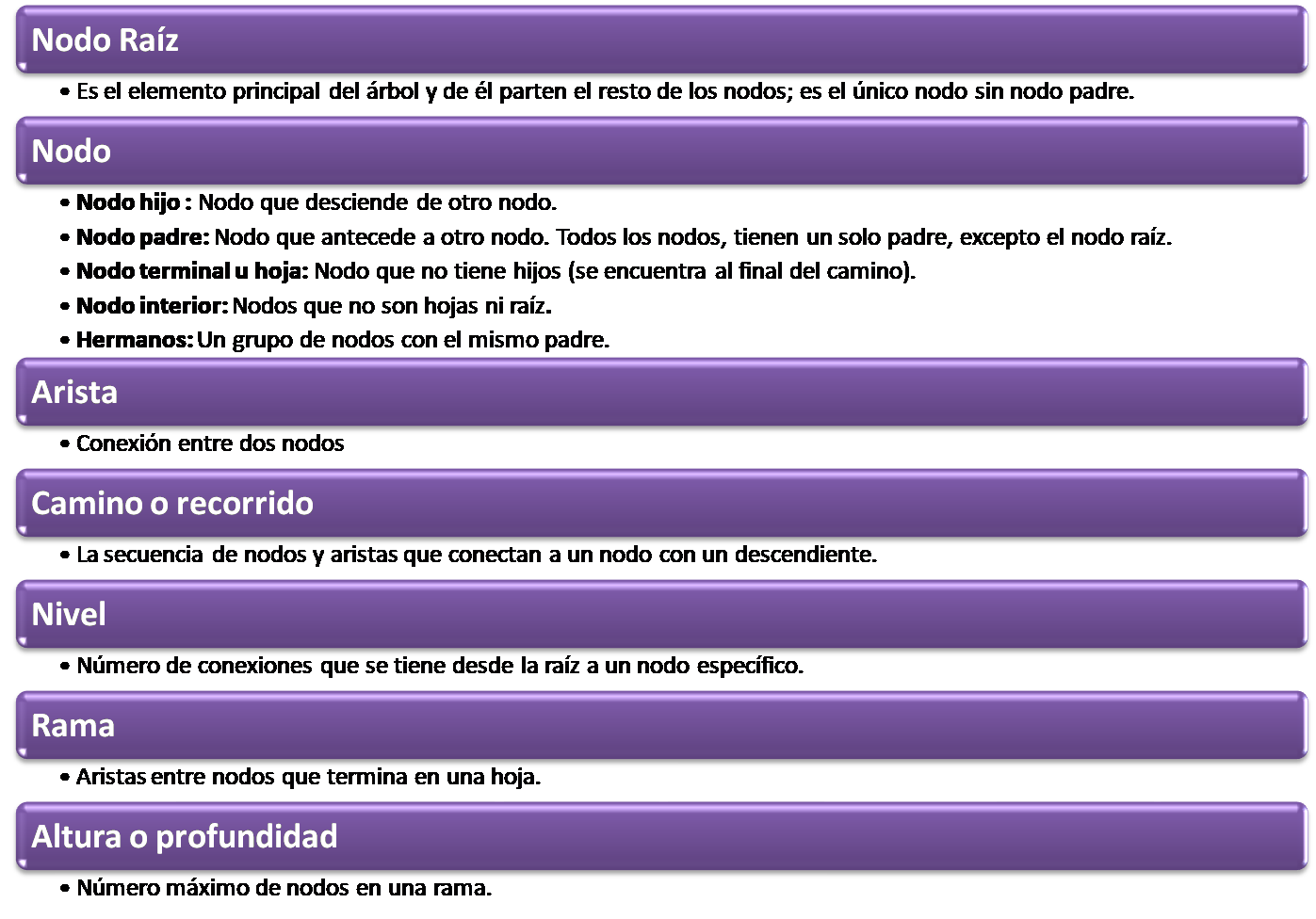
Fuente: propia (2020)
Definición del tipo de dato abstracto árbol binario
Un árbol binario, que podríamos representar con la letra T, se define como un conjunto finito de elementos llamados nodos, de forma que:

Fuente: propia (2020)
Continuamos un árbol binario en la estructura de datos, en la que puedes observar que:
- B es un sucesor izquierdo y C un sucesor derecho del nodo A.
- El subárbol izquierdo de la raíz A consiste en los nodos B, D y E, y el subárbol derecho de A consiste en los nodos C, F y G.

Fuente: propia (2020)
Continuando con nuestra descripción del árbol T, se puede deducir que:
- T es recursiva, ya que T se define en términos de los sub-árboles binarios T1 (Nodos B,D y E) y T2 (Nodos C,F yG). Esto significa, en particular, que cada nodo que llamaremos N de T contiene un subárbol izquierdo y uno derecho. Además, si N es un nodo terminal, ambos árboles están vacíos.
- Dos árboles binarios T y T' se dicen que son similares si tienen la misma estructura o, en otras palabras, si tienen la misma forma. Los árboles se dice que son copias si son similares y tienen los mismos contenidos en sus correspondientes nodos.
En la memoria de un sistema de cómputo, existen dos formas, que son las más utilizadas, de representar un árbol binario, a saber:
- Por medio de datos tipo puntero (apuntadores), también conocidos como variables dinámicas
- Por medio de arreglos
Las dos representaciones anteriores se pueden ver como un registro de datos, donde se tiene como mínimo tres campos:
- Uno en el que se almacenará la información del nodo.
- Otro que señala el árbol izquierdo del nodo actual.
- Un tercero que indica al árbol derecho del nodo actual.
A continuación en la siguiente imagen se muestra el campo de registro del Nodo N
Fuente: propia (2020)
En la imagen anterior vemos los 3 campos que se han mencionado en donde:
- IZQ: es el campo donde se almacenará la dirección del subárbol izquierdo del nodo T.
- Info: representa el campo donde se almacena la información del nodo. En este campo se pueden almacenar tipos de datos simples o complejos.
- DER: es el campo donde se almacena la dirección del subárbol derecho del nodo T.
A continuación, se observa un ejemplo de representación de un árbol binario:
Considérese un árbol binario que representa la expresión matemática (A * B) + ((C/D)^2). Su representación en memoria es la siguiente (Cairó y Guardati, 2006: 196).
En la siguiente imagen se representa la expresión matemática con un árbol binario:
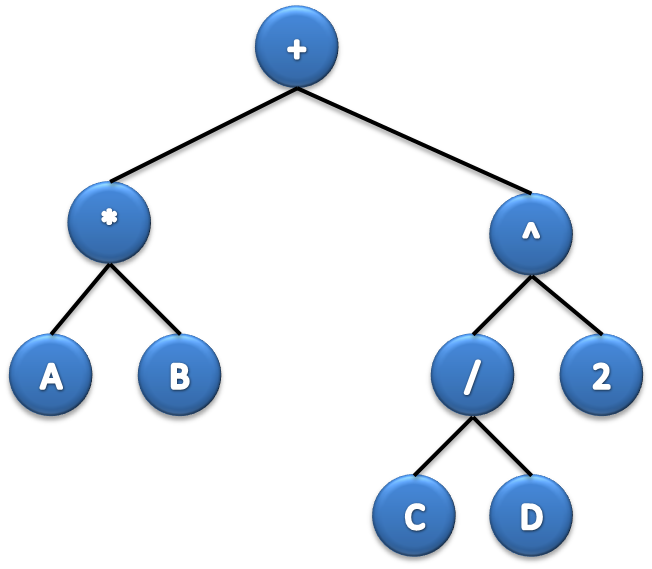
Programación de la Clase NodoArbol, en esta clase el NodoArbol vamos a crear dos variables una para la inserción de datos de tipo entero "dato" y a cada nodo se le asignará una cadena llamada "nombre", además la clase NodoArbol apuntará a al hijoIzq e hijoDer.
También construiremos un constructor NodoArbol que recibe un entero dato y una cadena nombre, les recuerdo la ventaja de los constructores son precisamente porque podemos inicializar las variables de lo que van a recibir por ello asignamos a this.dato=dato, this.nombre=nombre, los hijosIzq e hijoDer los inicializamos en null debido a que este método apuntará a un árbol vacío.
El método toString es un método que nos permite obtener información de las cadenas de caracteres y por tanto lo utilizaremos para mostrar lo que contiene dato y nombre.

Programación ArbolBinario, en la presente clase


Clase principal, ya que contiene el método main para que sea ejecutable

Grafos
Imagina que tienes una serie de destinos a los cuales quieres llegar, como diferentes estados de la República mexicana, y quieres saber cuál es la ruta más corta y más práctica para visitar todos los destinos en el menor tiempo y utilizando la menor cantidad de gasolina; éste tipo de problemas se pueden representar con grafos, en donde cada uno de los destinos son nodos y las rutas entre ellos son vértices en donde puedes manejar datos como, la distancia o la cantidad de gasolina que gastas de un punto a otro.
Definición del tipo de dato abstracto grafo
En palabras de Guardati (2007), los grafos son: " Estructuras de datos no lineales, en las cuales cada elemento puede tener cero o más sucesores, así como cero o más predecesores. Dichas estructuras están formadas por nodos o vértices (representan información) y por arcos o aristas (relaciones entre la información)."
Representación genérica de un grafo

Fuente: propia
Para poner un ejemplo de lo anterior, considera la representación de una red de carreteras entre diferentes ciudades, cada una de las ciudades representaría un nodo (vértice) del grafo y las carreteras los arcos (aristas). A cada arco se asociaría información como la distancia entre ciudades. Los grafos ayudan a esquematizar dicha información, como la que se mencionó anteriormente y que se representa como la figura anterior.
Por otro lado, existen diferentes tipos de grafos, los cuales se clasifican de acuerdo a lo que podrás observar en la siguiente imagen:
Clasificación de los tipos de grafos

Un grafo puede tener señalada una dirección o no. Cuando el grafo no señala ninguna dirección se llama grafo no dirigido, tal como se muestra en la siguiente imagen:
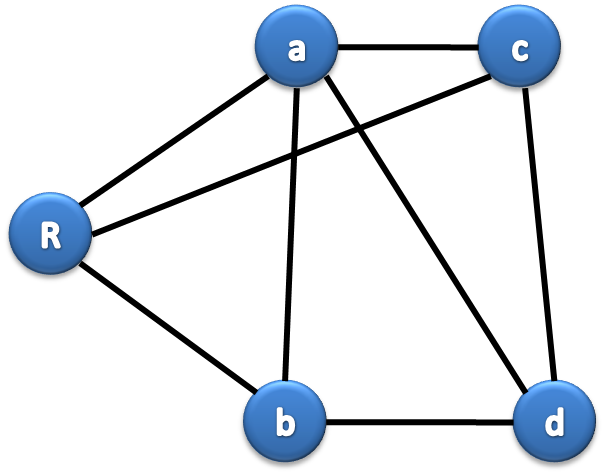
En un grafo dirigido o también conocido como dígrafo, el conjunto de sus aristas tiene una dirección.
Grafo dirigido

Los grafos ponderados son muy útiles, por ejemplo, para medir las distancias en un mapa. En el caso de un repartidor de muebles que tiene que recorrer varias ciudades de México conectadas entre sí por las carreteras que hay entre la Ciudad de México, Guadalajara y Monterrey, su misión es optimizar la distancia recorrida (minimizar el tiempo, prever tráfico y atascos). El grafo correspondiente tendrá como vértices estas ciudades y como aristas la red de carreteras y la valoración, peso o ponderación será la distancia que hay entre ellas.
Para tal efecto, es preciso atribuir a cada arista un número específico, ponderación, peso o coste según el contexto, y se obtiene así un grafo valuado o ponderado.
Grafo ponderado

Una de las formas de representar un grafo de cualquier tipo es a través de una matriz de adyacencias, ésta matriz puede representarse por medio de un arreglo de la siguiente forma.
Grafo representado como una matriz de adyacencias

En la figura anterior se observa que cada uno de los índices del arreglo representa uno de los nodos numerados del 1 al 5; en la matriz se representa la conexión entre nodos con un número 1 y con 0, aquéllos que no tienen conexión.
Otra forma de representar un grafo de cualquier tipo es a través de una lista de adyacencias de la siguiente forma; en donde cada lista representa los nodos adyacentes a un nodo en particular.
representado como una lista de adyacencias

En la figura anterior se representan las conexiones de cada uno de los nodos con una lista; por ejemplo, el nodo 4 tiene conexiones con los nodos 1, 3 y 5, por eso se forma una lista con dichas adyacencias y de la misma forma para el resto de los nodos.
Operaciones sobre un grafo
Las operaciones más básicas que debe tener un gafo, permiten agregar nodos y borrarlos, así como agregar aristas y borrarlas:
- Init(): Iniciar un grafo.
- addNodo(): Agregar nodo o vértice
addEdge(): Agregar arista
removeEdge(): Borrar arista
removeNode(): Borrar nodo o vértice
Implementación de un grafo
Con base en la representación que se revisó acerca de un grafo como una matriz de adyacencias, se revisará cómo expresar esa matriz en código de programación con Lenguaje C y las operaciones para la generación de grafos; en este caso sólo se estudiará la operación init()
Declaración de un grafo no dirigido en Lenguaje C, por medio de una matriz de adyacencias


